



 |
 |
 |
 |
 |
Workshop
Desafíos matemáticos e informáticos para la construcción y análisis de redes de regulación biológica
Universidad de Concepción, 22-23 de abril de 2016
El objetivo de este Workshop es compartir desafíos matemáticos e informáticos que se han observado en el modelamiento de las redes de regulación biológica. Para esto el comité organizador ha convocado a un encuentro que reúna científicos de distintas áreas, tales como biología, matemática e informática, para compartir sus problemas de investigación en un contexto interactivo que de pie a la discusión y la colaboración entre los participantes.
Comite organizador: Julio Aracena (DIM-UdeC), Anahí Gajardo (DIM-UdeC), Lilian Salinas (DIICC-UdeC), Christopher Thraves (DIM-UdeC).
Contacto: jaracena@ing-mat.udec.cl
| Sábado 23 de abril | |
|---|---|
| Hora | Actividad |
| 10:30-13:00 | Discusión |
| 13:00 | Almuerzo |
Presentaré informalmente la clase de autómatas totalísticos en dos dimensiones con la vecindad de von Neumann y estados {0, 1} de modo que al alcanzar el estado uno este permanece fijo. A tales autómatas se les asociará el problema de PREDICCION: dada una célula i en estado 0 y un step T ≥ 0, determinar si xi (T) = 1 (xi (t) = 0 para t < T).
Many proteins coordinate with others in groups called complexes in order to work together for achieving a specific function. In addition, many proteins are multifunctionals, therefore they participate in different protein complexes. We propose an efficient mining algorithm for discovering protein complexes based on detecting highly connected subgraphs that might overlap. Given that current Protein Protein Interaction Networks (PPIs) are unreliable (noisy and incomplete) and reference catalogues are also incomplete future research direction is in the analysis of false positives of complex prediction as well as in the discovery of other protein processes as in protein pathways.
La generación de modelos de Redes Regulación Transcripcional ha permitido entender desde una visión sistémica, como los organismos han desarrollado una compleja red molecular capaz de traducir diferentes estímulos en el control de la expresión génica. En su estructura más simple, estas redes se constituyen por proteínas reguladoras o factores de transcripción los cuales reconocen secuencias específicas en las regiones promotores de sus genes blanco. Si bien, las actuales estrategias permiten identificar y conectar un gran número de estos elementos, a la fecha no existe una herramienta definitiva para la construcción de redes de regulación transcripcional. En este contexto, desde el campo de la biología los actuales desafíos radican principalmente en: i) Generar modelos robustos y confiables a bajo costo, ii) Entender la operación de estas redes (estructura y funcionamiento). Como estrategia, el trabajo conjunto de diferentes laboratorios cuyo objetivo es combinar diversas capacidades científicas se proyecta como una alternativa eficiente para abordar estos desafíos.
Este trabajo está enfocado en determinar todos los problemas de clasificación de autómatas celulares (CA) en una dimensión que convergen sólo a los puntos fijos 0 y 1, presentando condiciones necesarias para esto.
Mostraremos resultados obtenidos para CA de radio 1 y 1.5 y plantearemos algunas propiedades que deseamos encontrar al aumentar el radio.
Dada una red Booleana que modela cierto fenómeno, conocer las dinámicas distintas que se obtienen producto de iterarla con diferentes esquemas de actualización deterministas permite, entre otras cosas, definir medidas que determinen el grado de robustez del modelo. En este contexto, se han establecido cotas superiores, en función de la topología de la red, para la cantidad de estas dinámicas distintas, sin embargo, encontrar redes que alcancen dichas cotas es un problema que ha sido poco estudiado. En esta presentación, mostraré que en la familia de los automatas celulares elementales (ECA) pareciera ser que lo anterior se cumple en 146 de los 256 ECAs posibles y, junto con ello, las conjeturas que debemos validar/refutar.
En esta presentación mostraremos resultados en complejidad computacional del autómata de mayoría en la grilla bi-dimensional con signos. Mostraremos que, dependiendo de la simetría y uniformidad de dichos signos, estos autómatas pueden simular distintos tipos de circuitos, y por lo tanto, presentar diferentes cotas inferiores en su complejidad. Concretamente, mostramos que los casos uniforme asimétrico y no-uniforme simétrico son Turing Universales (P-Hard); el caso no-uniforme asimétrico es intrínsecamente universal (PSPACE-Complete); y que ninguna regla simétrica uniforme puede ser intrínsecamente universal.
Complementamos estos resultados con ejemplos de ciclos de largo constante igual a dos, polinomial y super-polinomiales para los casos simétricos, anti-simétricos y asimétricos, respectivamente.
The neutral space is the collection of functional regulatory networks, obtained by reverse engineering techniques that contain a desired behavior/functionality. In this talk, evolutionary computation techniques to generate the neutral space through the construction of neutral networks will be addressed as well as some open problems.
Este trabajo se enfoca en encontar algoritmos eficientes que permiten encontrar esquemas de actualización deterministas que preservan ciertas características dinámicas de una red Booleana, por ejemplo, un ciclo límite. Hasta ahora hemos desarrollado un algoritmo que permite encontar estos esquemas de acualización para un tipo determinado de restricciones, pero aún tenemos dos temas pendientes: ampliar el tipo de restricciones y automatizar la captura de estas.
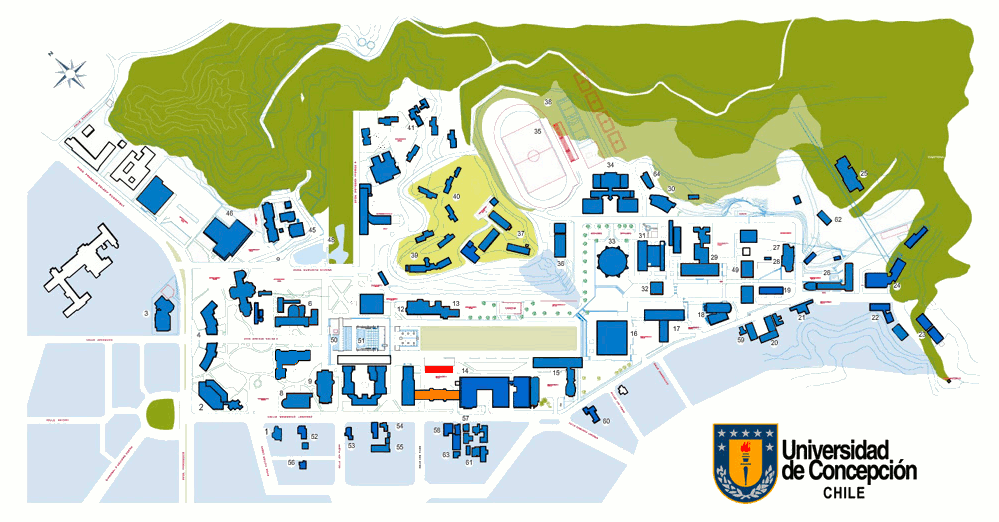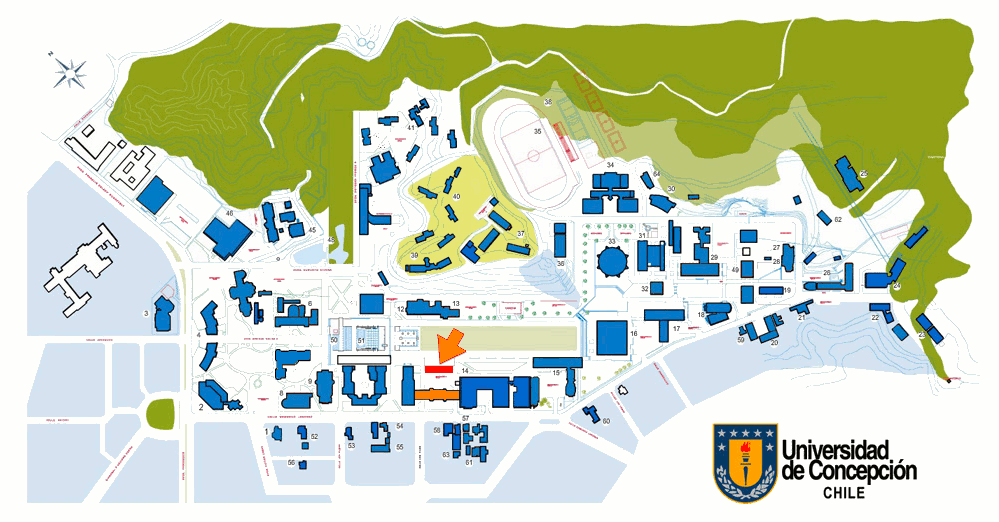
La charla Inaugural se realizará en el Auditorio 106, primer piso de la Facultad de Ingeniería (Edmundo Larenas 219) de la Universidad de Concepción. Las presentaciones se realizarán en la sala IS 3-1, tercer piso Edificio de Ingeniería de Sistemas.
Agradecemos el apoyo y el financiamiento aportado por: