Read, write and create datasets
In this section we provide functions to read and write our datasets, and create new ones.
Graphs
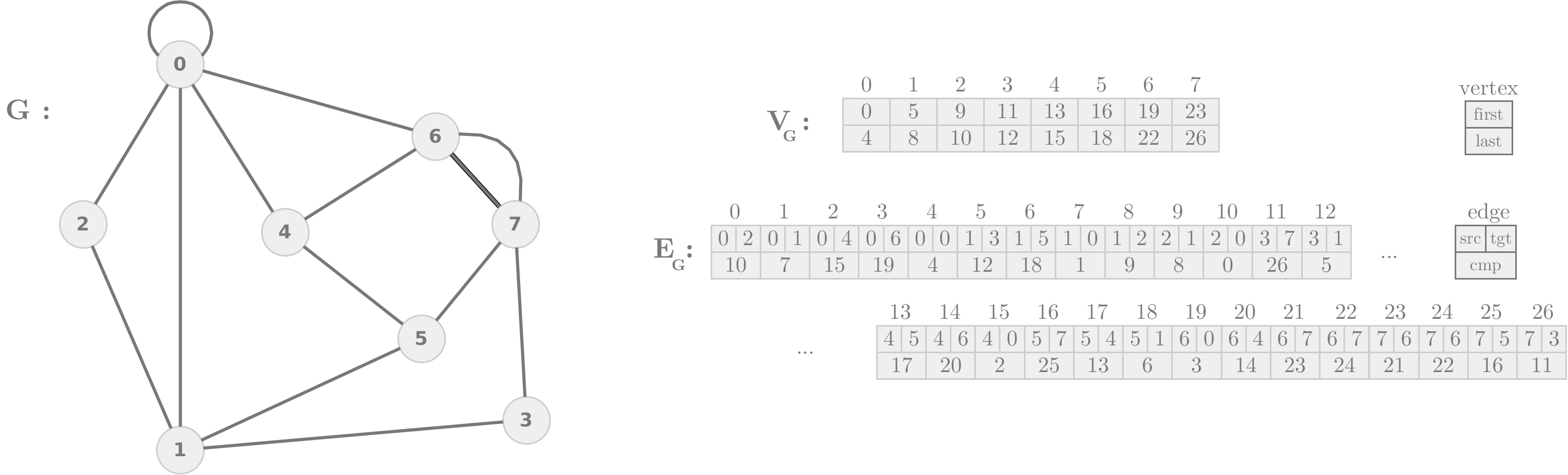
To navigate our graphs, we use the following representation:
Let G be a planar graph with a planar embedding. G is represented by an array of vertices, VG, and an array of edges, EG. Each vertex v ∈ V G stores two indices in EG, v.first and v.last, indicating the adjacency list of v, sorted counterclockwise around v. Notice that the number of neighbors of v is (v.last - v.first + 1). Each edge e ∈ EG has three fields, e.src, which is a pointer to the source vertex, e.tgt, which is a pointer to the target vertex and e.cmp, which is the position in EG of the complement edge of e, e', where the e'.src = e.tgt and e'.tgt = e.src. For example, see the following graph and its representation.

To support multiple edges, the indices of the multiple edges must be always increasing. In other words, the adjacency list of a vertex cannot start in the middle of a list of multiple edges.
- Read and write graphs: Read and write graphs. This code convert a graph from our datasets to the representation above.
- Build planar graphs: Build a planar graph with a planar embedding. We provide a set of scripts in bash and python to generate planar graphs based on Delaunay triangulations. To use the scripts, the following softwares have to be installed: Python3 (package numpy), Triangle and The Edge Addition Planarity Suite.
Trees
To navigate our trees, we use the same representation used in graphs. The only difference is that the adjacency list of a node starts with the edge to the parent of such node (except the root). Notice that the number of children of a node v is (v.last - v.first). For example, see the following tree and its representation.
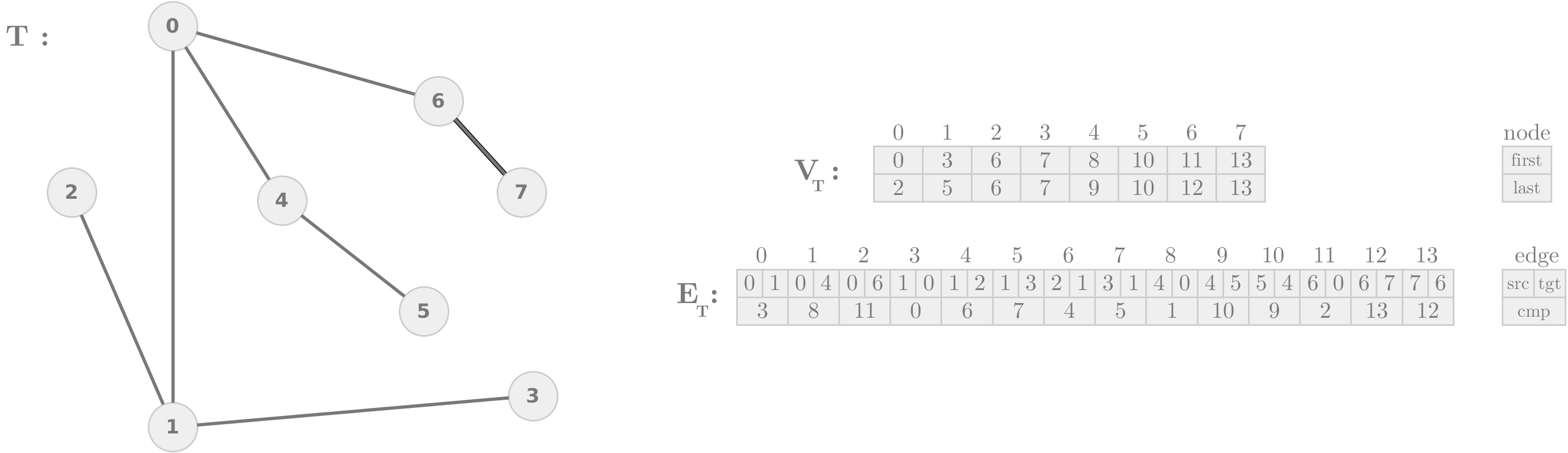
- Read and write trees: Read and write trees. This code convert a tree from our datasets to the representation above.
- Spanning tree of a graph: Compute a spanning tree of a graph, assuming the previous representations of graphs and tree.
Balanced parenthesis (BP) sequences
- Build BP complete bin tree: Build the balanced parenthesis sequence representation of a complete binary tree.
- Build BP suffix tree: Build the balanced parenthesis sequence representation of a suffix tree.
- Read and write BP sequences: Read and write balanced parenthesis sequences. This code convert a sequence of parentheses in text form to a bit array and vice versa. The bit array C library of Isaac Turner is used.