SPATIAL DATABASES

In the spatial domain, integrity constraints have been mainly used for preventing structural inconsistency (i.e., inconsistency between stored data and rules of geometric primitives), whereas conflicting information about positional information has been treated as a problem of data accuracy.

In addition to traditional integrity constraints, rules about spatial data must ensure consistent updating of spatial information (i.e., consistency of the geometric representation of objects with respect to a model of spatial information). A typical classification of these spatial constraints is:

• Topological constraints. Topological constraints are those constraints that address geometrical properties and spatial relations. They may be associated with structural considerations, such as that partitions only meet or are disjoint, or topological conditions, such as centerlines must meet at intersections.
• Semantic integrity constraints. These constraints are concerned with the meaning of geographic features; for example, landparcels are not contained in building-blocks.
• User-defined integrity constraints. These types of constraints are equivalent to business rules in non-spatial DBMS; for example, legal rules that constraints the installation of a gas station in a given region.

Like in traditional database systems, constraints at a conceptual and logical level in spatial databases are inherited by the implementation or physical level. These constraints are translated into a proprietary scripting language or into explicit constraints coded in the application programs

At a logical level, the definition of constraints based on topological relations. use a formal framework for defining topological relations. This framework defines topological relations between subsets of a classical topological space by the emptiness or non-emptiness of the two-by-two intersections of the subsets' interiors and boundaries.

.Within this framework, spatial relations and integrity constraints are expressed by using first-order logic. Atomic topological formulae in combination create topological sentences. Atomic topological formulae include geometric operators over objects, elementary topological relations between objects, and comparison between objects' attributes. For example, consider the following statement in natural language of a semantic integrity constraint in a cadastral application: land_parcels are not contained in building_blocks. The formal specification of this constraint for land_parcels lp and building_blocks bl based on the topological relations defined above is:

 

Some topological constraints define geometric primitives or some spatial dependences of composite objects. Consider, for example, partitions of a space. To define a partition rule in first-order logic, one needs to consider predicates of the type Pi(x), with x being an interior point of an object Pi. The spatial aggregation of partitions P0 ... Pn into W, assuming that partitions can only meet or be disjoint, where meet and disjoint were defined above

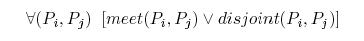
is then defined by the statement that a point $x$ in the aggregation must belong to one partition

 

A graph-based model of maps has also been used to establish topological integrity constraints of objects and their aggregations as a map. This model makes it possible to guarantee the consistency of a map through database updates with respect to a set of topological constraints over vertices, edges and faces on the map graph. Theses integrity constraints are equivalent to the mathematical axioms of maps that are defined by a graph that is plane, connected, nonseparable and formed by edges that are straight lines bounding internal faces.

---