5.2    Secuencia en expresiones aritméticas.

Consideremos la fórmula para calcular raíz cuadrada:

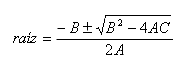
En un lenguaje de alto nivel como FORTRAN, la fórmula para una de las raíces se puede codificar casi directamente como una sola expresión:

La notación es compacta y natural, el procesador de lenguajes, en vez de el programador se ocupa del almacenamiento temporal y de la optimización.

Pero, ¿Cómo sabemos que la resta se hará después de calcular 4*A*C y no antes? Son los mecanismos de control de secuencia los que determinan el orden de las operaciones dentro de la expresión.

El mecanismo básico de control de secuencia en expresiones es la composición de funciones: se especifica una operación y sus operandos; los operandos pueden ser constantes, variables u otras operaciones, cuyos operandos, a su vez, pueden ser constantes, variables u otras operaciones, a cualquier profundidad. La composición de funciones da a la expresión la estructura característica de un árbol, donde la raíz representa la operación principal, los nodos intermedios representan operaciones de nivel intermedio y las hojas representan referencias de datos (constantes o variables).

Por ejemplo, nuestra expresión:

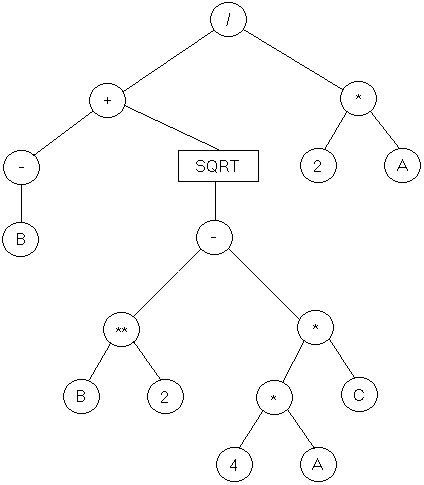
Es claro que los resultados de operaciones a niveles más bajos en el árbol sirven como operandos a operaciones de niveles más altos y por lo tanto las primeras deben ejecutarse antes de las segundas. Sin embargo, el árbol deja parte del orden de evaluación sin definir. Por ejemplo, no está claro si -B se debe evaluar antes de B**2, ni tampoco si las dos referencias a B se pueden combinar en una sola. Desafortunadamente en presencia de operaciones con efectos colaterales puede significar una diferencia.

Para poder usar esas expresiones en programas se requiere una linealización de los árboles. Examinemos las notaciones más comunes:

Notación prefija (polaca): Se escribe primero el nombre de la función seguida de los operandos de izquierda a derecha. Si un operando es a su vez operación con operandos, se aplican las mismas reglas. Por ejemplo:

* +ab -ca se obtiene recorriendo el árbol en forma pre-fija. En nuestro ejemplo anterior quedaría:

No hay ambiguedad alguna ni se necesitan paréntesis para saber como evaluar la expresión.

Debido a que el matemático polaco Lucasiewicz inventó la notación libre de paréntesis, se ha aplicado el término de polaca a esta notación y sus derivados.

Una variante de esta notación, que se usa en Lisp, a veces conocida como polaca de Cambridge, es un operador y sus argumentos encerrados entre paréntesis. Una expresión se ve como un conjunto anidado de listas, donde cada lista comienza con el operador seguido por las listas que representan los operandos. Por ejemplo:

En el caso de la raíz cuadrada quedaría:

Notación posfija (o polaca inversa): Es similar a la notación pre-fija, excepto que el símbolo de operación sigue a la lista de operandos. Por ejemplo:

que equivale a recorrer el árbol posorden. La expresión de la raíz cuadrada queda:

Notación infija: Es la más adecuada para operaciones binarias. El operador se escribe entre los operandos. Por su uso natural, ha sido adoptada por muchos lenguajes para operaciones aritméticas y lógicas. Cuando la operación no es binaria, se usa de manera algo torpe empleando varios delimitadores; por ejemplo el comando condicional en C:

Evaluación prefija: En esta notación se puede evaluar la expresión con un sólo examen de la misma, pero es necesario conocer el número de operandos de cada operación, por lo tanto se necesita diferenciar la resta binaria (-) del menos unario (-). Algunas de sus ventajas son:

1. Cualquier llamada usual a función está en notación prefija: f(x,y).
2. Se puede usar para representar operaciones de cualquier número de operandos, por lo que es general; solo es necesario aprender una regla sintáctica para escribir cualquier expresión. Por ejemplo: Lisp con notación polaca Cambridge.
3. Es fácil decodificar mecanicamente, lo que facilita su traducción.

Evaluación posfija: Cuando se examina un operador, sus operandos ya han sido evaluados, por lo tanto, la estrategia de evaluación es directa y fácil de implementar.

Evaluación infija: Aunque es común en los LP, su uso conduce a varios problemas:

1. Debido a que la notación infija es adecuada para operadores binarios, los LPs que la usan deben combinarla con notación prefija (o posfija); por lo que se complica la traducción.
2. Cuando aparece más de un operador infijo en una expresión, la notación es inherentemente ambigua, a menos que se usen paréntesis.

Por la razón 2, los LPs introducen, por lo general, reglas implícitas de control que hacen innecesario el uso de paréntesis. La jerarquía de operadores por lo general se asemeja al uso cotidiano. Ej: En Ada:

Frente a la asociatividad, por ejemplo: a-b-c es interpretado como (a-b)-c; sin embargo, la exponenciación opera de derecha a izquierda:

a^b^c = a^(b^c)

La precedencia funciona bastante bien en las expresiones usuales, pero a medida que los lenguajes evolucionan con nuevos operadores, estas precedencias dejan de funcionar.