Definición
 |
Una red Booleana es un sistema dinámico discreto introducido por Stuart Kauffman en 19691 para modelar Redes de Regulación génica. Pero, ¿qué son las redes de regulación génica? Los genes son partes de material genético y las redes de regulación génica se originan cuando este material genético interactúa, y de este modo permite que se activen o inhiban ciertas características en los seres vivos. Las redes Booleanas se transforman así en un modelo, o dicho en palabras más simples, en un juguete que permite predecir o reproducir parcialmente el comportamiento de una red de regulación génica. Para representar los genes se utilizan vértices los que se representan por un círculo, estos vértices pueden estar en estado activo (1) o inactivo (0). Las interacciones entre ellos se representan por funciones Booleanas, que dependen de los valores de otros vértices de la red. Esta dependencia se representa por flechas que van desde un vértice a otro o a sí mismo |
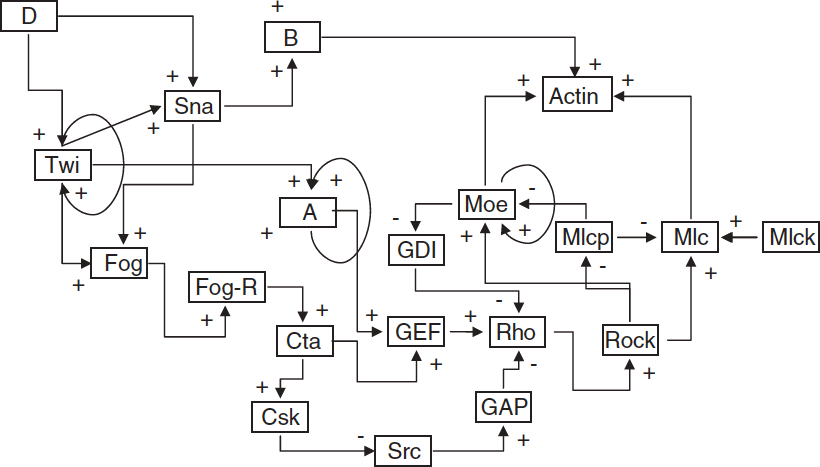
Aqí vemos un ejemplo de la red de regulación de la gastrulación de la Drosophila Melanogaster.2
 |
 |
Funciones Booleanas
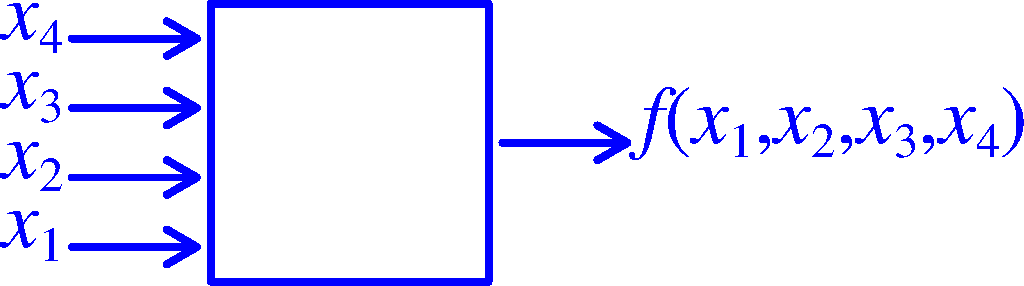 |
Una función Booleana es como una "cajita misteriosa" donde entran un conjunto definido de valores Booleanos (0 o 1) y sale como resultado un valor 0 o 1. Así como con los números usamos operaciones como la suma, la resta, la multiplicación y la división, para definir las funciones Booleanas usamos operaciones Booleanas. Existen muchas operaciones Booleanas, aquí presentamos cuatro con las cuales se puede construir cualquier función, estas son: la negación, disyunción, conjunción y disyunción exclusiva. A continuación se muestran las tablas que definen estas operaciones. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1Kauffman, S. A. Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of Theoretical Biology 22 (1969), 437-467.
2Aracena, J., Cambiazo, V., González, M., Méndez, M., Ramírez, P. Regulatory network for cell shape changes during Drosophila ventral furrow formation. Journal of Theoretical Biology 239 (2006), 49-62
Digrafo de interacción
 |
|
El digrafo de interacción de una red Booleana es una estructura compuesta por vértices que representan cada gen y por arcos que van del vértice i al vértice j, si la función del vértice j depende del vértice i. Diremos que la interacción es positiva, si cuando el vértice i aumenta de valor el valor del vértice j tiende a aumentar. La interacción es negativa, si cuando el vértice i aumenta de valor el valor del vértice j tiende a decrecer. Cuando no ocurre ninguna de las anteriores la interacción no tiene un signo definido. Cuando todas las interacciones tienen un signo definido, se dice que la red Booleana es definida por signo. Esta clase de funciones es muy importante ya que usualmente los modelos de redes regulatorias son definidas por signo. Decimos que un ciclo es positivo si tiene una cantidad par de arcos negativos y es negativo en caso contrario. |
Una característica importante del grafo de interacción es que permite conocer algunos aspectos del comportamiento dinámico de la red, sin necesidad de iterarla completamente. Algunos resultados conocidos son:
- Si el digrafo no tiene ciclos, hay único punto fijo.1
- Si al eliminar τ vértices del digrafo, se eliminan todos los ciclos, entonces la red tiene a lo más 2τ puntos fijos.2
- Si todos los ciclos son negativos, la red no tiene puntos fijos2
- Si todos los ciclos son positivos la red tiene al menos dos puntos fijos2
1Robert F. Discrete Iterations. Springer Series in Computational Mathematics 1986.
2Aracena J. Maximum Number of Fixed Points in Regulatory Boolean Networks. Bulletin of Mathematical Biology 70 (2008), 1398-1409.
Esquemas de actualización
¿Como hago que los vértices cambien su valor de estado? Si debo actualizar varios vértices en cada paso de tiempo existen varias maneras de hacerlo. Una primera alternativa es actualizarlos todos al mismo tiempo, es decir, cada vértice se actualiza con los valores que sus vértices de entrada tenían en el periodo anterior, esta manera la llamamos actualización paralela o sincrónica. Una segunda manera, es actualizar uno a la vez en algún orden preestablecido, esta manera la llamaremos actualización secuencial. Una tercera alternativa es agrupar los nodos en bloques de modo que al interior de cada bloque se actualiza de manera paralela y cada bloque tiene un cierto orden definido, esta manera la llamamos bloque secuencial.
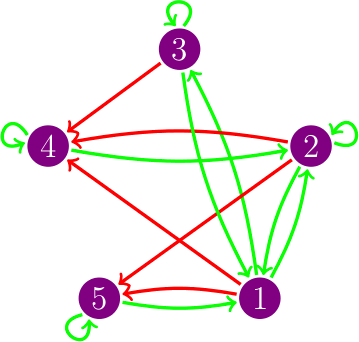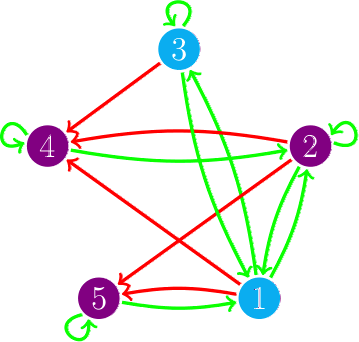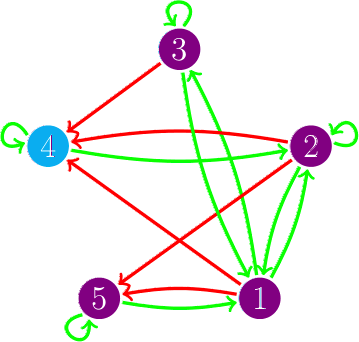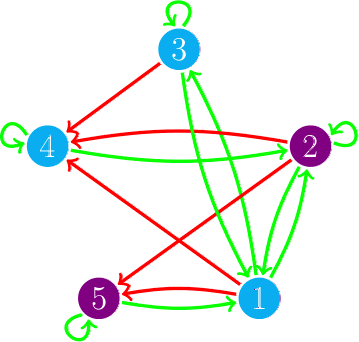
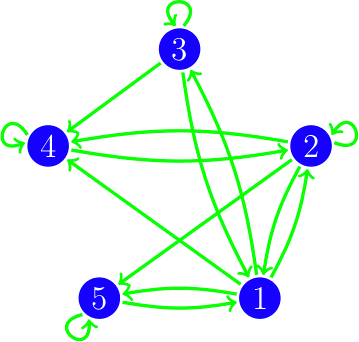
Este tipo de esquemas de actualización se puede representar coloreando los arcos del digrafo, si hay un arco de i a j y i se actualiza antes que j lo coloreamos rojo, si i se actualiza después o al mismo tiempo que j lo coloreamos verde; este grafo coloreado lo llamamos digrafo de actualización. En el dibujo vemos el digrafo de actualización del esquema de actualización s = {4, 5}{2}{1,3}, es decir, primero actualizamos al mismo tiempo los vértices 4 y 5, después actualizamos el vértice 2 y, por último, actualizamos 1 y 3 al mismo tiempo.
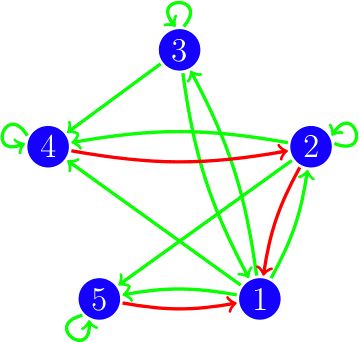 | 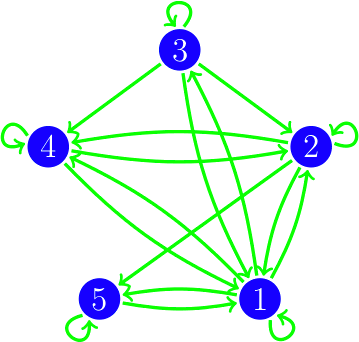 |
¿Cómo se hace esta actualización? Veamos el ejemplo de red de la sección anterior y actualicemos un estado de manera paralela, y también con un esquema bloque secuencial y uno secuencial.
Actualización paralela (s = {1, 2, 3, 4, 5})
En la actualización paralela cada vértice actualiza su estado, considerando el estado de los vértices en la etapa anterior. Luego si x0 = (0,0,0,0,1), entonces:
|
|
Por lo tanto, x1 = (0,1,1,0,1).
Actualización Bloque-Secuencial (s = {4, 5}{2}{1, 3})
En la actualización bloque-secuencial cada vértice actualiza su estado, considerando el estado de los vértices en la etapa anterior si es que estos están en el mismo bloque o uno posterior y en la etapa actual si están en un bloque anterior. Como para calcular el estado de 2 necesitamos el estado actualizado de 4 y 5 y para calcular es estado de 1 y 3 necesitamos los estados actualizados de 2, 4 y 5, debemos actualizar los vértices en el orden que aparecen en el esquema de actualización. Luego si x0 = (0,0,0,0,1), entonces:
|
|
Por lo tanto, x1 = (1,1,1,0,1).
Actualización Secuencial (s = {4}{5}{2}{3}{1})
En la actualización secuencial cada vértice actualiza su estado, considerando el estado de los vértices en la etapa anterior si es que estos están en un bloque posterior y en la etapa actual si están en un bloque anterior. Como para calcular el estado de 5 necesitamos el estado actualizado de 4, para 2 necesitamos 4 y 5 y así sucesivamente, debemos actualizar los vértices en el orden que aparecen en el esquema de actualización. Luego si x0 = (0,0,0,0,1), entonces:
|
|
Por lo tanto, x1 = (0,1,1,0,1).
Existen muchas otras formas de actualizar una red Booleana, por ejemplo al azar, es decir, en cada paso de tiempo actualizamos solo un vértice y para elegir cual simplemente lo dejamos al azar. Aquí, consideramos solo las primeras tres alternativas.
Es importante notar que la manera en la que actualizamos una red Booleana influye en su comportamiento, en particular influye en los atractores que alcanza.
Dinámica
 |
|
La dinámica de un red Booleana es el comportamineto que tiene la red al evolucionar siguiendo su regla de transición y su esquema de actualización. Un aspecto muy importante en la dinámica de una red son sus atractores. Hsciendo us de este ejemplo veremos como se calcula la dinámica de una red Booleana. |
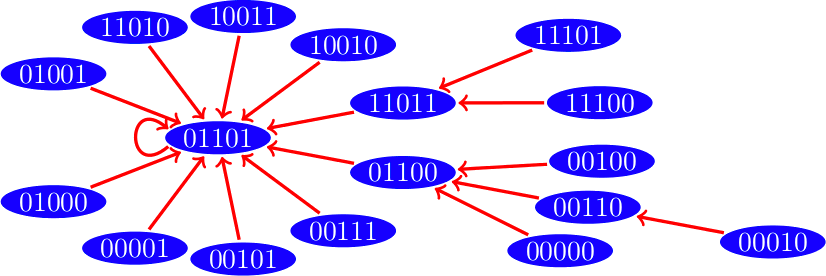
Dinámica con esquema de actualización paralelo
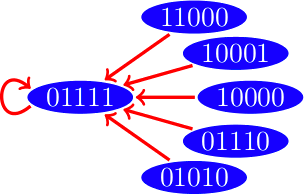 |
 |
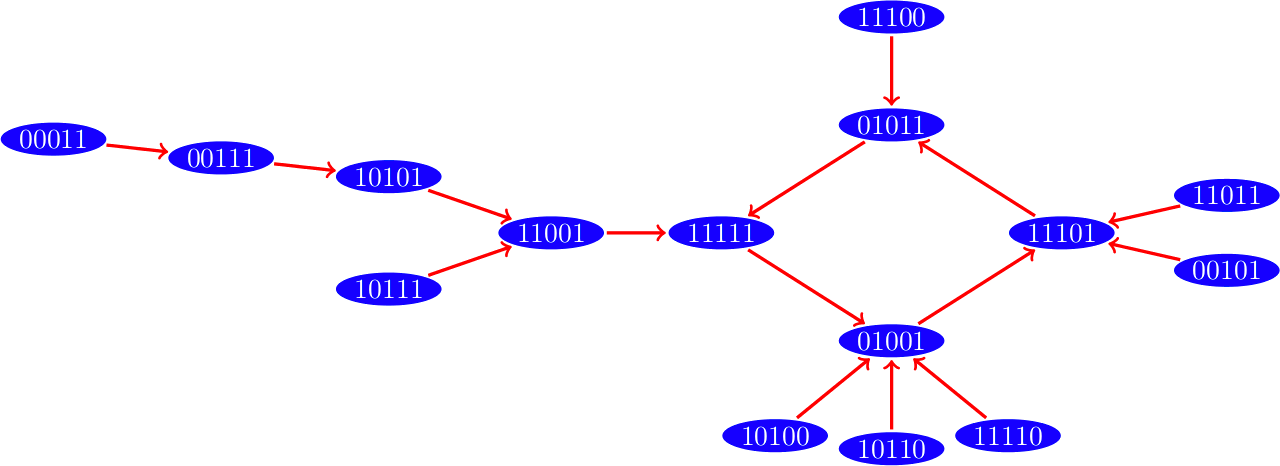 |
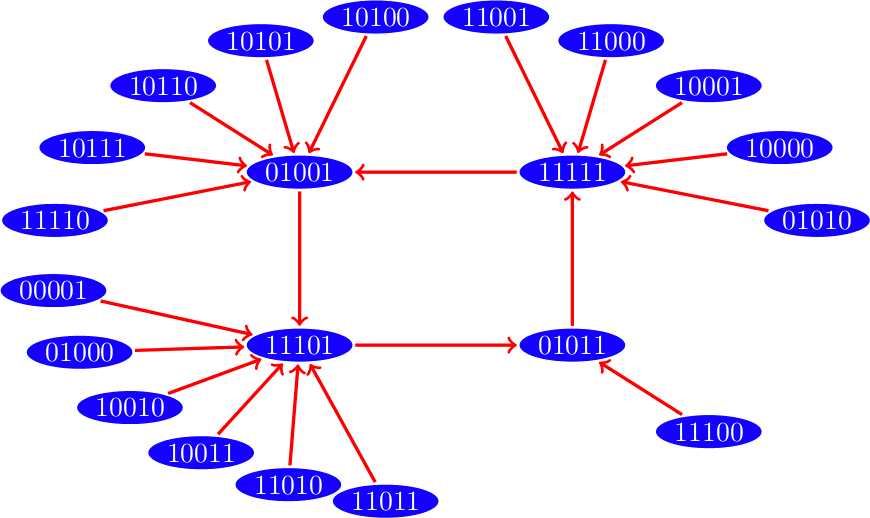
Dinámica con esquema de actualización bloque-secuencial
 |
 |
 |
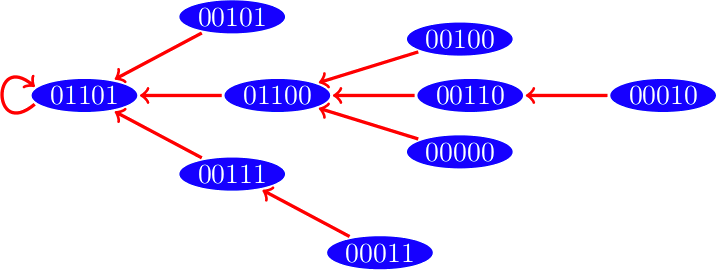
Dinámica con esquema de actualización secuencial
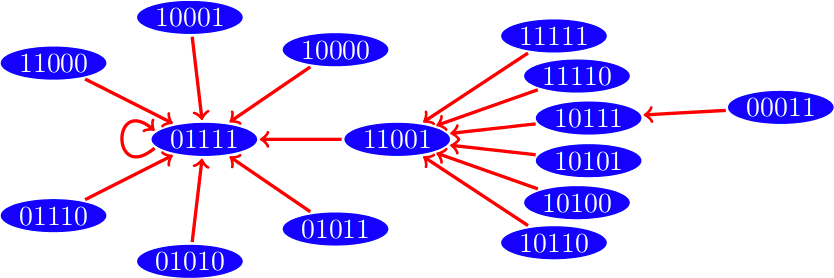 |
 |
Atractores
Hemos visto que una red Booleana tendrá un estado que corresponde a alguna configuración de ceros y unos de sus vértices, y estos estados cambian en cada paso de tiempo. Pero como los estados son una cantidad finita en algún momento estos se comenzarán a repetir, estos estados que se repiten infinitamente son lo que llamamos un atractor.
Existen dos tipos de atractores: los puntos fijos son estados cuyo estado siguiente es el mismo y los ciclos límite que son una colección de estados que pasan de uno al siguiente y se repiten infinitamente.
• = 1; • = 0
| Puntos fijos | Ciclos límite | |
|---|---|---|
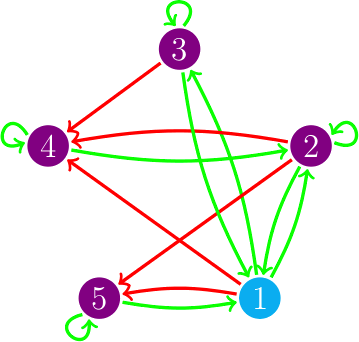 |
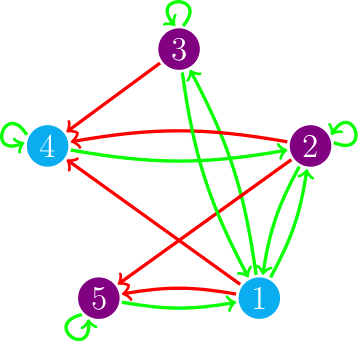 |
 |
Valles de atracción
El valle de atracción de un atractor son los estados de la red que llegan a este atractor.