| The peano representation combines space-filling with quad-trees. A space-filling
curve is an infinite sequence of curves, whose limit fills a given
square. This curves aims to map a two dimensional space onto a curve,
such that two points close in the space are close on the curve. The
quadtree is a generalized of the binary tree in which every node is a
leave of has four children. A quadtree partitions recursively the space
into 4 partitions until reaching a maximum granularity or having a
homogenous partition. A typical filling curve is the z-curve, which can be drawn at different levels of granualrity. 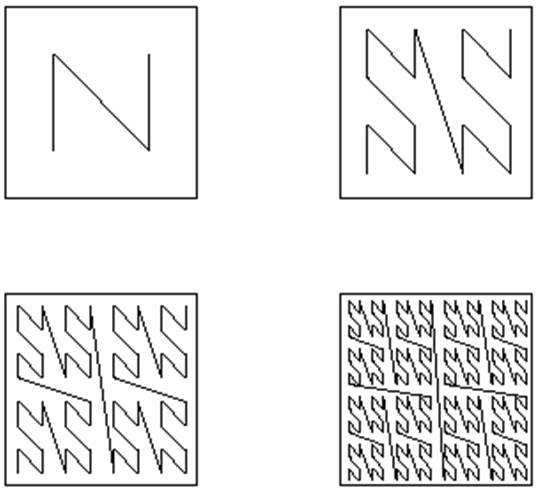 Based on the z-curve, partitions of the space are sequencely numbered. These numbers serves as identifications in the quadtree representation. Each node in the quadtree stores the attribute value, the (height - level) in the tree and the identification of the lower left cell in the partition. 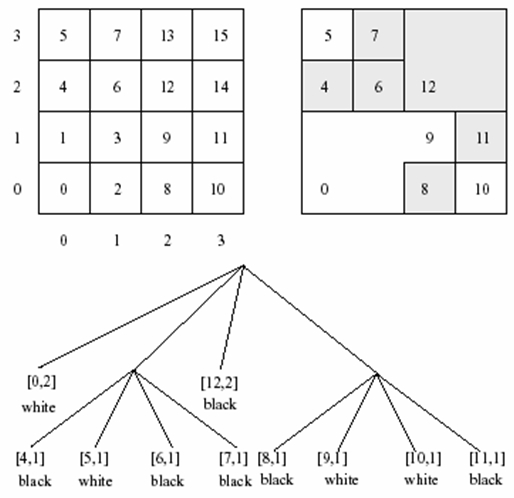 |
Última modificación: Wednesday, 9 de November de 2005, 05:25