SPATIAL DATABASES

<<< Previous

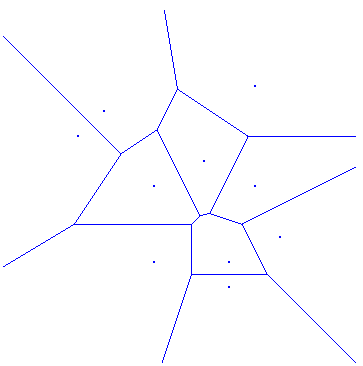
A well known way to partition the space is by the Voronoi tessellation. Voronoi represents a partition of space into regions. The dual of Voronoi is the Delaunay Triangulation that partitions the Euclidean space, composed of a set of points, into triangles such that no four points of this set are co-circular. In the Voronoi diagram, points of the Delaunay Triangulation are the nuclei of specific areas. These areas are bounded by the perpendicular bisectors of the nucleus and the set of its neighboring points.

Next >>>